Signal ou bruit ?

Une question récurrente quand on parle de série chronologique de valeurs issue d'un processus (ventes, défauts, visites, abonnements, temps de livraison, ...) :

Peut on distinguer entre un écart du au hasard d'une sur ou sous-performance ?

Tous les tableaux de bord affichent des séries de données. Tous les managers se saisissent de la valeur la plus récente et la compare à:

• la valeur précédente
• la valeur de l'an dernier à la même époque
• l'objectif
• l'avance/retard sur le cumulé à date
• ....

Positif ? Négatif ? En pourcentage ? Et là les ennuis commencent !! Faut il interpréter cet écart comme une variation de performance ou un simple bruit résultat de conjonction d’évènements hors de tout contrôle et somme toute normal ?

Beaucoup d'indicateurs utilisent les flèches haut/bas qui disent la variation avec la valeur précédente. C'est malheureusement une fausse bonne idée quand on l'applique sur une série chronologique soumise à des variations aléatoires. Combien de réunions de crise ou de célébrations ont été organisées sur la base de simples écarts à la moyenne ? Et à l'inverse combien auraient dues être organisées si une variation aléatoire n'avait pas masquée une tendance lourde à laquelle il aurait fallu réagir immédiatement ?

Le Process Behavior Chart

Inventé par Walter A. Shewhart en 1924 ce diagramme fait partie du domaine du Statistiscal Process Control. Repris par Deming, il est exploité dans beaucoup de démarche qualité (6 sigma). D'une simplicité désarmante, très robuste et d'une large applicabilité, cette technique prend la forme d'un graphe double qui rend visible les caractéristiques du processus. Il peut s'utiliser au fil de l'eau ou à postériori. Cette approche, pas très jeune, est modeste dans ses ambitions. Il n'y a pas volonté de prévoir ou d'expliquer, seulement d'observer, de constater et de s'ajuster. Regardons ce qu'il est possible d'en tirer. Le plus simple n'est il pas le meilleur ? Ou au moins à essayer en premier ?

La détection des valeurs anormales

Le signal est tracé sur sa moyenne (en pointillé) et est entouré d'une zone de variation "normale" (en bleu clair). Si un point en sort, il est dit "aberrant" (en rouge), un accident, un évènement exceptionnel, ... ou le signe précurseur d'un changement dans le processus de production des données ?

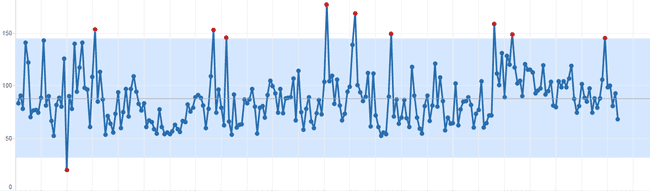
C'est là que le management peut lancer à juste titre une réunion d'analyse des causes. La largeur de la zone bleue est calculée à partir du signal lui même, elle est proportionnelle à la moyenne des variations d'une valeur à la suivante.

La détection de changements des caractéristiques du processus

Le diagramme permet de voir que le signal est en train de diverger de son gabarit calculé. Il propose un critère précis: l'apparition de 8 points successifs du même coté de la moyenne (en orange) indique que le signal a changé de mode et qu'il faut recalculer la moyenne et la zone de variation pour pouvoir continuer à l'interpréter correctement.

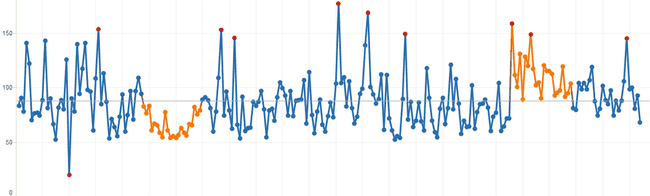
Le diagramme se transforme en une succession de moyennes et de zones admissibles qui donne un recul très informatif sur les données de base. L'œil se décolle de la courbe des valeurs individuelles et découvre le paysage global. Les bonnes questions surgissent: Pourquoi le signal a t il changé de nature à ce moment ? Est ce corrélé à un autre changement ? Pourquoi autant de hausse ? de baisse ?

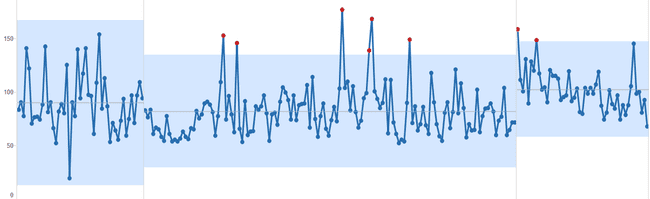
Le diagramme complet

Le Process Behavior Chart est en réalité double: Le signal comme vu précédemment et en dessous le diagramme de la suite des sauts entre valeurs successives.

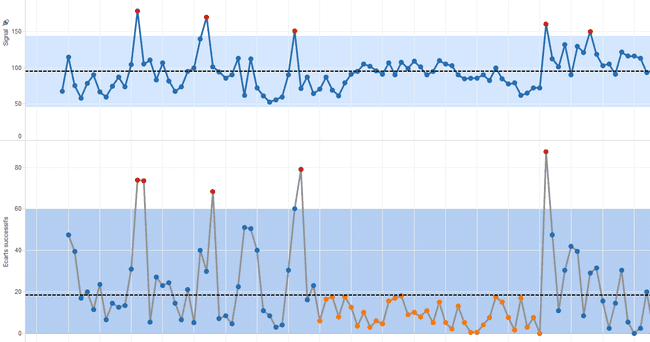
Le même procédé (moyenne, zone de variation, ...) s'applique à ce diagramme des variations et pour être complet, les valeurs aberrantes et les changements du processus, doivent se lire sur les deux diagrammes simultanément. Une valeur est aberrante si sa valeur s'écarte trop de la moyenne ou si la différence avec la valeur précédente est anormale. C'est aussi valable pour la détection d'un changement de mode à faire sur l'un OU l'autre des diagrammes. Sur l'exemple, le signal oscille autour de la moyenne, il ne déclenche pas la couleur orange. Par contre la diminution de l'amplitude de ses variations déclenche le critère des 8 points consécutifs sous la moyenne dans le diagramme du bas.
Après 10 minutes de formation, un néophyte complet est capable de lire et de raisonner sur un Process Behavior Chart.

Une référence lisible sans aucun bagage statistique que je recommande: Wheeler, Donald J. (2000). Understanding Variation: the key to managing chaos ou encore les Nelson Rules.